OptimaBlog

Hidden Markov Model

Introducción:

Los modelos de estados ocultos de Markov (HMM, por sus siglas en inglés) son herramientas estadísticas que se utilizan para modelar sistemas dinámicos en los que los estados no son directamente observables, pero se pueden inferir a partir de observaciones indirectas. En el contexto de los activos financieros, los HMM pueden ser utilizados para modelar el comportamiento de los precios de los activos a lo largo del tiempo.

En un modelo de HMM aplicado a un activo financiero, los "estados ocultos" representan las condiciones latentes o no observables del mercado. Estos estados podrían corresponder, por ejemplo, a diferentes regímenes de mercado, como un mercado alcista, bajista o lateral, o podrían representar diferentes niveles de volatilidad.

Estas "observaciones" en un modelo de HMM son las señales o datos disponibles sobre el activo financiero, como los precios de cierre diarios, el volumen de operaciones, los indicadores técnicos, etc.

La idea fundamental detrás de los HMM es que el estado latente del mercado influye en las observaciones observadas, pero no se puede observar directamente. Sin embargo, a través de técnicas de inferencia estadística, como el algoritmo de Viterbi o el filtro de Kalman, es posible estimar la secuencia más probable de estados latentes dados los datos observados.

Estos modelos pueden ser útiles en una variedad de aplicaciones financieras, como la predicción de precios de activos, la identificación de cambios en el régimen del mercado, la gestión del riesgo y la toma de decisiones de inversión. Por ejemplo, un inversor podría utilizar un modelo de HMM para ajustar su estrategia de inversión según el régimen actual del mercado, o un gestor de riesgos podría utilizar un HMM para evaluar la probabilidad de eventos extremos en los precios de los activos.

Estructura del Modelo de Markov Oculto (HMM):

Un HMM es un modelo probabilístico que describe una secuencia de observaciones a través del tiempo, donde cada observación es el resultado de un estado oculto subyacente. La estructura básica de un HMM incluye:

Estados Ocultos (Hidden States): Representan las condiciones latentes o no observables del sistema. En un modelo de Markov, se asume que el estado actual solo depende del estado anterior, lo que se conoce como la propiedad de Markov. Los estados ocultos forman una cadena de Markov.
Observaciones (Observations): Son las señales o datos que se observan directamente. Cada estado oculto genera una distribución de probabilidad sobre las posibles observaciones.
Matriz de Transición de Estados (Transition Matrix): Es una matriz que describe las probabilidades de transición entre los estados ocultos. Cada elemento 𝑎𝑖𝑗aij de la matriz representa la probabilidad de pasar del estado 𝑖i al estado 𝑗j.
Matriz de Emisión (Emission Matrix): Es una matriz que describe las probabilidades de observar cada posible observación dado un estado oculto. Cada elemento 𝑏𝑖𝑗bij de la matriz representa la probabilidad de observar la observación 𝑗j dado el estado 𝑖i.
Distribución Inicial de Estados (Initial State Distribution): Es la distribución de probabilidad inicial sobre los estados ocultos en el tiempo 𝑡=0t=0.

Algoritmo de Viterbi:

El algoritmo de Viterbi es un algoritmo de programación dinámica que se utiliza para encontrar la secuencia de estados más probable en un modelo de Markov oculto (HMM) dado un conjunto de observaciones. Es particularmente útil cuando se trabaja con HMMs, ya que permite encontrar eficientemente la secuencia de estados más probable sin tener que considerar todas las posibles combinaciones de estados.

Aquí tienes una descripción del algoritmo de Viterbi y sus ecuaciones:

Inicialización:
- Inicializa una matriz llamada 𝛿δ de tamaño 𝑇×𝑁T×N, donde 𝑇T es el número de pasos de tiempo y 𝑁N es el número de posibles estados del HMM.
- Calcula el valor inicial de 𝛿δ para el primer paso de tiempo usando la distribución inicial de estados del HMM y la probabilidad de observar la primera observación dada cada estado.
Recursión:
- Para cada paso de tiempo 𝑡t de 22 a 𝑇T:
  - Para cada estado 𝑗j de 11 a 𝑁N:
    - Calcula el valor de 𝛿𝑡(𝑗)δt(j) como el máximo de la expresión:𝛿𝑡(𝑗)=max⁡𝑖=1𝑁[𝛿𝑡−1(𝑖)×𝑎𝑖𝑗×𝑏𝑗(𝑜𝑡)]δt(j)=i=1maxN[δt−1(i)×aij×bj(ot)]
    - Donde:
      - 𝛿𝑡−1(𝑖)δt−1(i) es el valor de 𝛿δ en el paso de tiempo anterior para el estado 𝑖i.
      - 𝑎𝑖𝑗aij es la probabilidad de transición del estado 𝑖i al estado 𝑗j.
      - 𝑏𝑗(𝑜𝑡)bj(ot) es la probabilidad de observar la observación 𝑜𝑡ot dado el estado 𝑗j.
Terminación:
- La secuencia de estados más probable se encuentra retrocediendo en la matriz 𝛿δ desde el último paso de tiempo 𝑇T. Selecciona el estado con el valor más alto en 𝛿𝑇(𝑗)δT(j) como el último estado de la secuencia.
- Retrocede hacia atrás a través de la matriz 𝛿δ utilizando los valores de 𝛿δ y las probabilidades de transición para determinar el estado más probable en cada paso de tiempo anterior.
- Este proceso proporciona la secuencia de estados más probable dada una secuencia de observaciones en un modelo de Markov oculto. Es importante tener en cuenta que el algoritmo de Viterbi es altamente eficiente y solo requiere tiempo proporcional a 𝑇𝑁2TN2 para calcular la secuencia de estados más probable, donde 𝑇T es el número de pasos de tiempo y 𝑁N es el número de estados posibles del HMM.

Relación entre el Modelo de Markov Oculto y el Algoritmo de Viterbi:

El algoritmo de Viterbi es una forma eficiente de encontrar la secuencia más probable de estados ocultos en un HMM, dado un conjunto de observaciones. Utiliza la propiedad de Markov y las probabilidades de transición y emisión del modelo para calcular esta secuencia de manera óptima. Entonces, el modelo de Markov oculto define la estructura subyacente del sistema, mientras que el algoritmo de Viterbi proporciona una forma de inferir los estados ocultos más probables dadas las observaciones disponibles.

Aplicación ejemplificada de Viterbi y Markov

Supongamos que tenemos un HMM que modela el estado del tiempo (soleado, nublado, lluvioso) y que solo podemos observar si las personas llevan o no un paraguas (sí o no). Queremos usar el algoritmo de Viterbi para determinar la secuencia más probable de estados del tiempo dado un conjunto de observaciones sobre si las personas llevan un paraguas durante varios días.

Aquí están las probabilidades de transición entre los estados del tiempo y las probabilidades de observación:

Probabilidades de transición entre estados:
- Soleado a soleado: 0.7
- Soleado a nublado: 0.2
- Soleado a lluvioso: 0.1
- Nublado a soleado: 0.3
- Nublado a nublado: 0.4
- Nublado a lluvioso: 0.3
- Lluvioso a soleado: 0.2
- Lluvioso a nublado: 0.4
- Lluvioso a lluvioso: 0.4
Probabilidades de observación:
- Soleado y llevando un paraguas: 0.1
- Soleado y sin llevar un paraguas: 0.9
- Nublado y llevando un paraguas: 0.6
- Nublado y sin llevar un paraguas: 0.4
- Lluvioso y llevando un paraguas: 0.9
- Lluvioso y sin llevar un paraguas: 0.1

Supongamos que tenemos la siguiente secuencia de observaciones durante tres días: llevando un paraguas, llevando un paraguas, no llevando un paraguas.

Ahora aplicaremos el algoritmo de Viterbi para encontrar la secuencia más probable de estados del tiempo.

Inicialización:
- Inicializamos la matriz 𝛿δ con valores iniciales basados en la distribución inicial de estados y la primera observación.
Recursión:
- Calculamos los valores de 𝛿δ para los siguientes pasos de tiempo utilizando las ecuaciones del algoritmo de Viterbi.
Terminación:
- Encontramos la secuencia de estados más probable retrocediendo a través de la matriz 𝛿δ desde el último paso de tiempo.

Para este ejemplo simplificado y sencillo, el algoritmo de Viterbi nos estaría dando la secuencia más probable de estados del tiempo dado las observaciones sobre si las personas llevan un paraguas durante esos días.

HMM aplicado a finanzas, una introducción

Supongamos que queremos modelar los movimientos del S&P 500 en tres estados: "Alcista" (↑), "Bajista" (↓) y "Lateral" (↔). Utilizaremos un modelo de Markov de primer orden, lo que significa que el estado futuro depende solo del estado actual y no de los estados anteriores.

Matriz de transición de estados (A): Esta matriz describe las probabilidades de transición entre los estados. Por ejemplo, podría tener la forma:

A= [[ p↑∣↑, p↑∣↓, p↑∣↔,

p↓∣↑, p↓∣↓,p↓∣↔,

p↔∣↑, p↔∣↓, p↔∣↔ ]]

Donde 𝑝𝑖𝑗pij representa la probabilidad de pasar del estado 𝑖i al estado 𝑗j. Por ejemplo, 𝑝↑∣↑p↑∣↑ sería la probabilidad de permanecer en un mercado alcista dado que el mercado está actualmente alcista.

Distribución inicial de estados (π): Esto representa la probabilidad de que el mercado esté en cada estado al comienzo del período de modelado. Por ejemplo, podría ser:

π= [[ π↑

π↓

π↔]]

Donde 𝜋↑π↑, 𝜋↓π↓ y 𝜋↔π↔ son las probabilidades iniciales de que el mercado esté en cada estado respectivamente.

Distribución de observaciones (B): Esto describe las probabilidades de observar ciertas señales (por ejemplo, cambios de precio, volumen de operaciones, etc.) dados los estados del modelo. En un modelo simple, podría ser una matriz de probabilidades fijas

La matriz de distribución de observaciones 𝐵 en un modelo de Markov oculto (HMM) describe las probabilidades de observar ciertas señales dados los estados del modelo. Matemáticamente, si tenemos N estados ocultos en nuestro modelo y M posibles observaciones, entonces la matriz B tendrá dimensiones N x m

Cada elemento bij de la matriz B representa la probabilidad de observar la señal j dado que el modelo está en el estado oculto i. Es decir, bij=P(Ot=j∣Qt=i), donde 𝑂𝑡 es la observación en el tiempo t y 𝑄𝑡 es el estado oculto en el tiempo t

En un modelo simple, esta matriz de distribución de observaciones puede ser una matriz de probabilidades fijas. Por ejemplo, si tenemos un HMM con 3 estados ocultos y 2 posibles observaciones, la matriz B podría tener la siguiente forma:

B =
[ 0.8 0.2
0.4 0.6
0.7 0.3 ]

En esta matriz, cada fila representa las probabilidades de observar las dos señales dado un estado oculto. Por ejemplo, en la primera fila, b_{11} = 0.8 indica la probabilidad de observar la primera señal dado el primer estado oculto, y b_{12} = 0.2 indica la probabilidad de observar la segunda señal dado el primer estado oculto.

Entonces de lo precedente podemos sumarizar que, la matriz de distribución de observaciones B en un HMM especifica cómo las observaciones se relacionan con los estados ocultos y proporciona información sobre cómo las señales observadas pueden influir en los estados ocultos del modelo.

Resultados de aplicación financiera

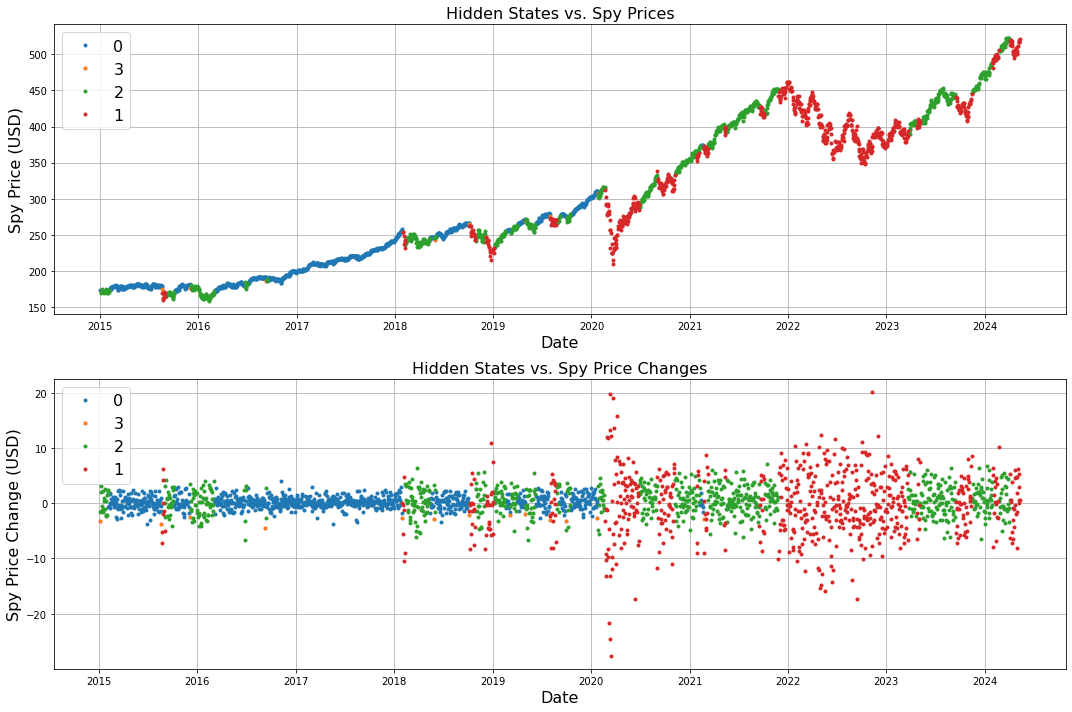
En el código de Python donde construimos y clasificamos estados del SP500, obtenemos como resultado estas conclusiones:

### ========================================

Unique states: [0 3 2 1]

Matriz de transición: Estado 0 Estado 1 Estado 2 Estado 3 Estado 0 0.984615 0.000000 0.001099 0.014286 Estado 1 0.000000 0.977376 0.022624 0.000000 Estado 2 0.016927 0.014323 0.968750 0.000000 Estado 3 0.000000 0.384615 0.615385 0.000000

Frecuencia de cada estado: 0 910 1 664 2 768 3 13

Name: count, dtype: int64

Número total de cambios de estado: 66

Longitud promedio de secuencia de estados consecutivos: 35.15

Start probabilities: [2.17374454e-126 1.25839418e-063 5.12224857e-036 1.00000000e+000]

Gaussian distribution means: [[ 0.21616373] [-0.27595145] [ 0.53097481] [-2.77608542]]

Gaussian distribution covariances: [[[ 1.10915942]] [[32.9373667 ]] [[ 5.95695789]] [[ 0.61104555]]]

### ====================================================

Unique states:
- Aquí se muestran los estados únicos que se han identificado en tus datos. En tu caso, los estados son etiquetados como 0, 1, 2 y 3.
Matriz de transición:
- Esta matriz muestra las probabilidades de transición entre los estados. Cada fila representa el estado actual y cada columna representa el próximo estado. Por ejemplo, en la fila "Estado 0", la probabilidad de permanecer en el Estado 0 es de aproximadamente 0.985 (98.5%), la probabilidad de cambiar al Estado 2 es de aproximadamente 0.001 (0.1%), y así sucesivamente. Lo mismo se aplica a las otras filas.
Frecuencia de cada estado:
- Esta salida muestra cuántas veces aparece cada estado en tus datos. Parece que el Estado 0 aparece 910 veces, el Estado 1 aparece 664 veces, el Estado 2 aparece 768 veces y el Estado 3 aparece solo 13 veces.
Número total de cambios de estado:
- Indica cuántas veces ocurre un cambio de estado en tus datos. En tu caso, parece que hay 66 cambios de estado.
Longitud promedio de secuencia de estados consecutivos:
- Esta es la longitud promedio de las secuencias de estados consecutivos en tus datos. En promedio, tus secuencias de estados consecutivos tienen una longitud de aproximadamente 35.15.
Start probabilities:

Estas son las probabilidades iniciales de comenzar en cada estado. Parece que hay una alta probabilidad de comenzar en el Estado 3 (casi 100%).
Medias de la Distribución Gaussiana (Gaussian Distribution Means):

Estos son los valores medios de las distribuciones gaussianas asociadas a cada estado oculto. Por ejemplo, el primer valor (0.21616373) representa la media de la distribución gaussiana asociada al primer estado oculto, el segundo valor (-0.27595145) representa la media del segundo estado oculto, y así sucesivamente.

Covarianzas de la Distribución Gaussiana (Gaussian Distribution Covariances):
- Estas son las matrices de covarianza de las distribuciones gaussianas asociadas a cada estado oculto. En el contexto de una distribución gaussiana multivariada, la covarianza describe la relación entre las diferentes dimensiones de los datos. Sin embargo, en este caso, parece que estamos tratando con distribuciones gaussianas univariadas, por lo que las matrices de covarianza son matrices diagonales con solo un elemento en cada fila y columna. Por ejemplo, el primer valor (1.10915942) en la primera matriz de covarianza representa la varianza de la distribución gaussiana asociada al primer estado oculto.

Estos valores definen las características estadísticas de las distribuciones gaussianas asociadas a cada estado oculto en el modelo de Markov oculto. Estos parámetros se utilizan para modelar la relación entre los estados ocultos y las observaciones en el modelo HMM.

Código de Python con explicación

## ===================================
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import yfinance as yf
from sklearn.mixture import GaussianMixture
from hmmlearn import hmm

### =====================================

# Define el símbolo del futuro del activo que deseas obtener
futuro_oro = yf.Ticker("SPY")

# Obtener los datos históricos del futuro del activo

data = futuro_oro.history(start="2015-01-01", end="2024-05-13")

# Restablecer el índice de datos para que la columna "Date" se convierta en el índice

data.reset_index(inplace=True)

# Use the daily change in gold price as the observed measurements X.

X = data[["Close"]].diff().dropna().values # Selecciona la columna "Close" y calcula la diferencia

# Crear un modelo GMM

n_components = 4 # Número de componentes en el modelo GMM
gmm = GaussianMixture(n_components=n_components, covariance_type="diag", random_state=42)
gmm.fit(X)

# Extraer los parámetros del modelo GMM
means = gmm.means_
covars = gmm.covariances_
weights = gmm.weights_

# Crear un modelo de Markov oculto personalizado utilizando los parámetros del GMM

model = hmm.GaussianHMM(n_components=n_components, covariance_type="diag", n_iter=50, random_state=42)
model.means_ = means
model.covars_ = covars
model.startprob_ = np.ones(n_components) / n_components # Probabilidades iniciales uniformes
model.transmat_ = np.ones((n_components, n_components)) / n_components # Matriz de transición uniforme

# Ajustar el modelo de Markov oculto a los datos

model.fit(X)

# Predict the hidden states corresponding to observed X.

Z = model.predict(X)

# Asegurarse de que Z tenga la misma longitud que los datos originales

if len(Z) == len(data) - 1:
Z = np.insert(Z, 0, 0) # Insertar un valor ficticio al principio para igualar la longitud

states = pd.unique(Z)

print("Unique states:")
print(states)

# Ajuste para el código existente...
plt.figure(figsize=(14, 7))
for i, (state, color) in enumerate(zip(range(n_components), ["red", "green", "blue", "orange"])):
# Filtrar las fechas donde el estado oculto es igual a 'i'
idx = (Z == state)

# NO es necesario ajustar los índices de data['Date'] y data['Close'] aquí

plt.plot(data['Date'][idx], data['Close'][idx], '.', color=color, label=f'Estado {state}')
plt.title('Precio de cierre del futuro del oro y estados predichos')
plt.legend()
plt.show()

# 1. Construir la matriz de transición

n_states = len(np.unique(Z)) # Número de estados únicos
# Inicializar la matriz de transición con ceros
transition_matrix = np.zeros((n_states, n_states))

# Llenar la matriz de transición

for (i, j) in zip(Z[:-1], Z[1:]):
transition_matrix[i, j] += 1

# Convertir conteos a probabilidades

transition_matrix = transition_matrix / transition_matrix.sum(axis=1, keepdims=True)

# Crear DataFrame para la matriz de transición para mejor visualización

transition_df = pd.DataFrame(transition_matrix,
columns=[f'Estado {i}' for i in range(n_states)],
index=[f'Estado {i}' for i in range(n_states)])

print("Matriz de transición:")
print(transition_df)

# 2. Calcular la frecuencia de cada estado
state_counts = pd.Series(Z).value_counts().sort_index()
print("\nFrecuencia de cada estado:")
print(state_counts)

# 3. Calcular la secuencia de estados consecutivos antes de un cambio

state_changes = (np.diff(Z) != 0).sum()
total_states = len(Z)
average_sequence_length = total_states / (state_changes + 1) # +1 para incluir la primera secuencia

print(f"\nNúmero total de cambios de estado: {state_changes}")
print(f"Longitud promedio de secuencia de estados consecutivos: {average_sequence_length:.2f}")

#Visualizar los cambios en el precio del activo asi como los precios de cierre

plt.figure(figsize=(15, 10))
plt.subplot(2, 1, 1)
plt.plot(data["Date"], data["Close"])
plt.xlabel("Date")
plt.ylabel("Gold Price (USD)")
plt.grid(True)
plt.title("Daily Gold Prices")
plt.subplot(2, 1, 2)
plt.plot(data["Date"], data["Close"].diff())
plt.xlabel("Date")
plt.ylabel("Gold Price Change (USD)")
plt.grid(True)
plt.title("Daily Gold Price Changes")
plt.tight_layout()
plt.show()

print("\nStart probabilities:")
print(model.startprob_)

#Start probabilities:
#[1.00000000e+00 4.28952054e-24 1.06227453e-46]

print("\nTransition matrix:")
print(model.transmat_)
#Transition matrix:
#[[8.56499275e-01 1.42858023e-01 6.42701428e-04]
#[2.43257082e-01 7.02528333e-01 5.42145847e-02]
#[1.33435298e-03 1.67318160e-01 8.31347487e-01]]

print("\nGaussian distribution means:")
print(model.means_)

#Gaussian distribution means:
#[[0.27988823]
#[0.2153654 ]
#[0.26501033]]

print("\nGaussian distribution covariances:")
print(model.covars_)

#Gaussian distribution covariances:
#[[[ 33.89296208]]

#[[142.59176749]]

#[[518.65294332]]]

plt.figure(figsize=(15, 10))
plt.subplot(2, 1, 1)
for i in states:
want = (Z == i)
x = data["Date"][want]
y = data["Close"][want]
plt.plot(x, y, '.')
plt.legend(states, fontsize=16)
plt.grid(True)
plt.xlabel("Date", fontsize=16)
plt.ylabel("Spy Price (USD)", fontsize=16)
plt.title("Hidden States vs. Spy Prices", fontsize=16)
plt.subplot(2, 1, 2)
for i in states:
want = (Z == i)
x = data["Date"][want]
y = data["Close"].diff()[want]
plt.plot(x, y, '.')
plt.legend(states, fontsize=16)
plt.grid(True)
plt.xlabel("Date", fontsize=16)
plt.ylabel("Spy Price Change (USD)", fontsize=16)
plt.title("Hidden States vs. Spy Price Changes", fontsize=16)
plt.tight_layout()
plt.show()

Este código realiza varias operaciones relacionadas con el análisis de datos financieros utilizando un modelo de Markov oculto (HMM) y un modelo de mezcla gaussiana (GMM). Aquí está el desglose del código:

Importación de bibliotecas:
- Importa las bibliotecas necesarias, incluyendo NumPy, Pandas, Matplotlib, yfinance (para obtener datos financieros) y las clases GaussianMixture y GaussianHMM de sklearn.mixture y hmmlearn, respectivamente.
Obtención de datos históricos:
- Utiliza la biblioteca yfinance para obtener datos históricos del futuro del índice SPY (S&P 500) desde el 1 de enero de 2015 hasta el 13 de mayo de 2024.
Preprocesamiento de datos:
- Restablece el índice de datos para que la columna "Date" se convierta en el índice.
- Calcula los cambios diarios en el precio de cierre y los almacena en la variable X.
Modelo de Mezcla Gaussiana (GMM):
- Crea un modelo de GMM con un número de componentes especificado (n_components) y lo ajusta a los datos de cambios diarios en el precio de cierre.
- Extrae los parámetros del modelo GMM, incluyendo las medias, las covarianzas y los pesos.
Modelo de Markov Oculto (HMM):
- Crea un modelo de HMM Gaussiano con el mismo número de componentes que el GMM y lo inicializa con los parámetros del GMM.
- Ajusta el modelo HMM a los datos de cambios diarios en el precio de cierre.
- Predice los estados ocultos correspondientes a las observaciones de precio de cierre.
Análisis y visualización:
- Realiza varias operaciones de análisis y visualización de los datos y los resultados del modelo, incluyendo la visualización de los precios de cierre y cambios de precios, la construcción de la matriz de transición, el cálculo de la frecuencia de cada estado, y la visualización de la relación entre los estados ocultos y los precios de cierre.

Además, se puede agregar más características al modelo para mejorar su capacidad predictiva. Por ejemplo, podríamos agregar la volatilidad como una característica adicional, de esta forma:

## ======================================

# Calculate volatility as an additional feature

data['Volatility'] = data['Close'].rolling(window=20).std() # Calculate 20-day rolling standard deviation as volatility

X = data[['Close', 'Volatility']].diff().dropna().values # Use both close price and volatility as features

## ==================================================

Finalización

Llegamos al final del post, esta ha sido una sencilla e informativa explicación financiera, matemática y estadística de la composición, estructura y funcionamiento aplicado de los HMM .

Además se proporcionó un sencillo algoritmo, para poder interactuar y visualizar los modelos ocultos de markov con Python.

Debe tener en cuenta el lector, que para nada es este código proporcionado una herramienta definitiva y pulida para operar en los mercados financieros, ya que esto conlleva una minuciosa y extensiva categorización e investigación de estructuras adicionales, como el riesgo, rentabilidad, backtesting, despliegue y automatización.

Este post fue redactado por Gabriel Gastón Guardia. Co Fundador de Optima Consulting & Managemet.

Contacto : gonzalezguardia.618@gmail.com

Para más contenido Quant en Python para Finanzas seguime en YouTube :

GQuant (@NietzscheanStocks)

Optima Consulting & ManagementHidden Markov Models for Finance