Optima Consulting & ManagementK- Nearest Neighbors Classification

Sea τ = {(xi, yi)} n i=1 el conjunto de entrenamiento, con yi ∈ {0, . . . , c − 1}, y sea x un nuevo vector de características. Definimos x(1), x(2), . . . , x(n) como los vectores de características ordenados por cercanía a x en alguna distancia dist(x, xi), por ejemplo, la distancia euclidiana ||x−xi||. Sea τ(x) := {(x(1), y(1)), . . . , (x(K), y(K))} el subconjunto de τ que contiene K vectores de características xi que están más cerca de x. Entonces, la regla de clasificación de los k-vecinos más cercanos clasifica x de acuerdo con las etiquetas de clase más frecuentes en τ(x). Si dos o más etiquetas reciben el mismo número de votos, el vector de características se clasifica seleccionando una de estas etiquetas al azar con igual probabilidad. Para el caso K = 1, el conjunto τ(x) contiene solo un elemento, digamos (x0, y0), y x se clasifica como y0. Esto divide el espacio en n regiones.

Ri = {x : dist(x, xi) 6 dist(x, xj), j , i}, i = 1, . . . , n.

Para cada punto de datos xi en un conjunto de datos, Ri representa el conjunto de todos los puntos x en el espacio de características que están más cerca de xi que de cualquier otro punto xj en el conjunto de datos. Es decir, Ri contiene todos los puntos x que están más cerca de xi que de cualquier otro punto en el conjunto de datos. Este concepto se conoce como región de Voronoi o célula de Voronoi.

Para un espacio de características R^p con la distancia euclidiana, esto genera una teselación de Voronoi del espacio de características. Una teselación de Voronoi divide el espacio en regiones poligonales, donde cada región está asociada con un punto de datos en el conjunto de datos original. Estas regiones se construyen de manera que cada punto dentro de una región esté más cerca del punto asociado que de cualquier otro punto en el conjunto de datos.

Ahora situamos, una explicación detallada:

1. Conjunto de Entrenamiento (τ): τ es el conjunto de datos de entrenamiento que contiene pares (xi, yi), donde xi son los vectores de características y yi son las etiquetas de clase correspondientes. En este contexto, n es el número total de observaciones en el conjunto de entrenamiento.
2. Nuevo Vector de Características (Feauters) (x): x es un nuevo vector de características para el cual queremos predecir la etiqueta de clase.
3. Vecinos más Cercanos (KNN): El método KNN clasifica un nuevo punto de datos basándose en la clase de sus vecinos más cercanos en el espacio de características.
4. Distancia entre Puntos (dist): dist(x, xi) es una medida de distancia utilizada para determinar qué puntos son los "vecinos más cercanos" de x. Comúnmente, se utiliza la distancia euclidiana, pero también se pueden utilizar otras medidas de distancia, como la distancia de Manhattan o la distancia de Mahalanobis.
5. Subconjunto de Vecinos más Cercanos (τ(x)): τ(x) es el subconjunto de τ que contiene los K vectores de características xi que están más cerca de x según la medida de distancia especificada.
6. Regla de Clasificación: La regla de clasificación de KNN determina la etiqueta de clase de x basándose en las etiquetas de clase de los puntos en τ(x). En otras palabras, clasifica x según la clase que es más común entre los vecinos más cercanos.
7. Desempate de Clases: Si dos o más clases reciben el mismo número de votos entre los vecinos más cercanos, la regla de clasificación puede elegir una de estas clases al azar con igual probabilidad.
8. Caso K = 1: Cuando K = 1, la clasificación se basa en el vecino más cercano único. En este caso, τ(x) contiene solo un elemento y x se clasifica como la clase de ese vecino más cercano. Esto significa que cada punto se asigna a la clase del punto más cercano.
9. División del Espacio: El proceso de clasificación divide el espacio de características en regiones distintas basadas en las etiquetas de clase de los vecinos más cercanos. Cada región está asociada con una clase específica.

En términos simples podemos ver un ejemplo,el algoritmo de clasificación de K-Vecinos más Cercanos (KNN) es bastante intuitivo. Imaginemos que tenemos un montón de puntos en un espacio, cada uno representando un objeto con diferentes características, y cada objeto tiene una etiqueta que indica a qué grupo pertenece. Por ejemplo, podrían ser puntos que representan diferentes tipos de frutas, y las etiquetas indican si son manzanas, naranjas, etc.

Cuando llega un nuevo punto (digamos, una nueva fruta cuyas características queremos clasificar), el algoritmo KNN mira a sus K vecinos más cercanos de los puntos que ya conocemos (esos puntos con sus etiquetas). Luego, mira qué etiquetas tienen esos vecinos y escoge la etiqueta más común entre ellos. Esa es la etiqueta que asigna al nuevo punto.

Por ejemplo, si estamos clasificando una fruta desconocida y vemos que de los 5 frutos más cercanos, 3 son etiquetados como manzanas y 2 como naranjas, entonces clasificarías la nueva fruta como una manzana.

El número K es una especie de "ventana" que define cuántos vecinos cercanos mirar para hacer la clasificación. Si K es igual a 1, entonces solo se mira al vecino más cercano para decidir la etiqueta.

En adición, el algoritmo también divide el espacio de características en diferentes regiones. Esto significa que hay áreas donde, por ejemplo, si tenemos una nueva fruta, probablemente sea una manzana porque todas las frutas cercanas son manzanas.

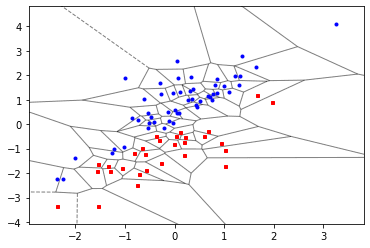
Por último generamos un código de Python para poder visualizar el algoritmo del vecino más cercano divide el espacio en celdas de Voronoi.

## ================================================##

import numpy as np
from numpy.random import rand, randn
import matplotlib .pyplot as plt

from scipy.spatial import Voronoi, voronoi_plot_2d

np.random.seed (12345)
M = 80
x = randn(M ,2)
y = np.zeros(M) # pre-allocate list

for i in range (M):
if rand()<0.6:
x[i,1], y [i] = x[i,0] + np.abs(randn()), 0
else:
x[i,1], y[i] = x[i ,0] - np.abs(randn ()), 1

vor = Voronoi(x)
plt_options = {'show_vertices':False , 'show_points':False ,
'line_alpha':0.5}
fig = voronoi_plot_2d (vor , ** plt_options )
plt.plot(x[y==0 ,0] , x[y==0 ,1] ,'bo',
x[y==1 ,0] , x[y==1 ,1] ,'rs', markersize =3)

## =====================================##

Este artículo fue publicado por Gabriel Gastón Guardia. Co Fundador de Optima Consulting & Management LLC.

Canal de YouTube: GQuant