Optima Consulting & ManagementStatistical Arbitrage : Test Dickey - Fuller con LSTM (Long Short Term Memory)

Primero que nada, ¿qué es la Cointegración y por qué es tan importante para el Statistical Arbitrage?

Una estrategia de Pairs Trading, involucra una posición Larga o Long contra una Corta, Short, al mismo tiempo en dos activos altamente correlacionados.

Ahora bien, ¿correlación entre qué? ¿Precios, retornos? Correlación entre retornos. Los precios de los activos a menudo no son
estacionarios y su correlación conducirá a conclusiones espurias.

Y entonces, ¿ cómo definimos la relacion entre el precio de los activos?Si, COINTEGRACIÓN.

Veamos la definición de Cointegración:

𝑥𝑡 y 𝑦𝑡 son cointegrados si 𝑥𝑡 y 𝑦𝑡 son series 𝐼(1) y existe un 𝛽 tal que 𝑧𝑡 = 𝑥𝑡 − 𝛽𝑦𝑡 es una serie 𝐼(0).

Entre las propiedades de la cointegración tenemos que:

Los precios de los activos cointegrados están vinculados debido a la estacionariedad de su spread.

• La cointegración es una medida de similitud de activos en términos de perfiles de exposición al riesgo.

• La cointegración describe una relación a largo plazo entre los precios de los activos; la correlación es una relación a corto plazo entre los rendimientos.

• La cointegración especifica la proporción de la pierna larga a la pierna corta, 𝛽.

La cointegración especifica la proporción de la Long Leg a la Short Leg, 𝛽.

• ¿Cómo encontrar 𝛽?

• Prueba de Engle-Granger (adecuada para un par de activos)

• Regresión lineal sobre los precios de los activos y prueba si el residual es estacionario

• Desventaja: ¿Qué activo elegir como variable dependiente? • Prueba de Johansen (adecuada para dos o más activos)

• Modelo de Corrección de Errores Vectoriales (VECM)

• Método preferido para probar la cointegración y derivar 𝛽.

En esta ocasión vamos a usar el test Dickey Fuller.

Ahora, cuando no tengo los datos pero aun así quiero probar las propiedades de la cointegración de pares, ¿qué hago?

Simular.

¿Por qué simular?

Es posible que no sepas dónde encontrar un par de activos cointegrados. • El S&P 500 tiene 505 componentes.

• 127,260 pares para considerar → ¡No factible!

• La simulación es omnipresente en el desarrollo de estrategias comerciales.

• Fijación de precios de opciones

• Backtesting de Monte Carlo

• La cointegración no es una excepción

Simulación: Proceso AR(1) estacionario

• Si una serie temporal es estacionaria, entonces debe ser una serie 𝐼 0
• Simular series 𝐼 0 con proceso AR(1) estacionario
𝑎𝑡 = 𝜑𝑎𝑡−1 + 𝜀𝑡 , I𝜑I < 1
Donde 𝜀𝑡 ∼ 𝑁(0, 𝜎2)

• Dos componentes son series 𝐼 (0)
• Retornos de un activo
• Spread de los pares cointegrados

¿Podemos simular un algoritmo de Statistical Arbitrage ahora? Vamos a ver.

Cointegrated Spread Simulation:

1. Simula el logaritmo del precio del activo Y, 𝑦𝑡, de manera que 𝑦𝑡 − 𝑦𝑡−1 = 𝑎𝑡 + 𝑐1, donde 𝑎𝑡 es un AR(1) estacionario.
2. Suma 𝑎𝑡 y obtén el logaritmo del precio del activo Y.
3. Simula el spread cointegrado entre el activo X y el activo Y, de modo que 𝑥𝑡 + 𝛽𝑦𝑡 = 𝑏𝑡 + 𝑐2, donde 𝑏𝑡 es un AR(1) estacionario.
4. Recupera el logaritmo del precio del activo X, 𝑥𝑡, calculando 𝑥𝑡 = 𝑏𝑡 − 𝛽𝑦𝑡.

Detallado esto, podemos desarrollar una estrategia de reversión a la media con pares de activos cointegrados.

Un breve repaso antes de continuar, tener en cuenta: ¿Qué estamos operando y qué estamos optimizando en esa operatoria?

El spread entre los activos cointegrados es de reversión a la media.

• La estrategia comercial es intuitiva: operar en contra de los extremos, es decir, "comprar barato, vender caro".

• Factor 1: ¿Dónde iniciar las operaciones? (Ubicación de la Operación)

• Determina la ganancia o pérdida mínima por operación.

• Factor 2: ¿Con qué frecuencia se realizan las operaciones? (Frecuencia de Operación)

• Determina el número de operaciones en un cierto período de tiempo.

• Objetivo de Optimización: Ubicación de la Operación × Frecuencia de Operación

Es decir, límites más estrechos, ganancia mínima por operación más pequeña, mayor frecuencia de operación. Por otra parte, límites más amplios, ganancia mínima por operación mayor, menor frecuencia de operación.

Entonces, debemos establecer una ganancia mínima por operación si o sí, de manera poder satisfacer las condiciones de riesgo y rentabilidad de la estrategia:

• Supongamos que el límite superior es 𝑈 > 0, y el coeficiente cointegrado de los activos 𝑋 e 𝑌 es 𝛽, es decir, 𝜀𝑡 = 𝑋 − 𝛽𝑌 es una serie 𝐼(0).

• Cuando 𝜀𝑡 ≥ 𝑈, abrir una operación vendiendo 𝑁 del activo 𝑋 y comprando 𝛽𝑁 del activo 𝑌.

• Cuando 𝜀𝑡 ≤ 𝐸[𝜀𝑡], cerrar la operación.

• Establecer un límite inferior simétrico para más operaciones.

Podemos definir la estrategia de trading así:

• Si 𝜀𝑡 ≥ 𝑈, vender 𝑁 del activo 𝑋, comprar 𝛽𝑁 del activo 𝑌.

• Si 𝜀𝑡 ≤ 𝐸[𝜀𝑡], cerrar la operación.

• Si 𝜀𝑡 ≤ 𝑈, comprar 𝑁 del activo 𝑋, vender 𝛽𝑁 del activo 𝑌.

• Si 𝜀𝑡 ≥ 𝐸[𝜀𝑡], cerrar la operación.

Obteniendo por trade un porfit definido por la siguiente expresión:

Profit per trade

𝑃 = 𝑁 (𝑋𝑜 − 𝑋𝑐) + 𝛽𝑁(𝑌𝑐 − 𝑌𝑜)

= 𝑁 (𝑋𝑜 − 𝛽𝑌𝑜) − 𝑁(𝑋𝑐 − 𝛽𝑌𝑐)

= 𝑁𝜀𝑡𝑜 − 𝑁𝜀𝑡𝑐 ≥ 𝑁U

La ganancia mínima por operación, al negociar 1 unidad del spread, es exactamente el valor del límite 𝑼.

Nota: La ganancia mínima es terminal.

Frecuencia de Operación: Tiempo Medio de Primer Paso

• Supongamos que el spread cointegrado, 𝜀𝑡, entre el activo 𝑋 y el activo 𝑌 es un proceso AR(1) estacionario.
• Utiliza el tiempo medio de primer paso del proceso AR(1) para optimizar la duración de la operación y el intervalo entre operaciones.
• Duración de la operación: el tiempo medio de primer paso de 𝜀𝑡 para pasar la media 𝐸[𝜀𝑡], si el punto de partida está en 𝑈.
• Intervalo entre operaciones: el tiempo medio de primer paso de 𝜀𝑡 para pasar 𝑈, si el punto de partida está en la media 𝐸[𝜀𝑡].
• Iguala la media a cero para facilitar el cálculo.

Podemos calcular entonces la duración de cada trade, y el Inter-trade interval, definidos respectivamente por:

Por supuesto, aquí está la adaptación:

\[ E_{T_{0,\infty}}[U] = \lim_{{b\to\infty}} \frac{1}{b} \int_{0}^{b} E_{T_{0,b}}[s] \exp \left( -\frac{(s - \phi U)^2}{2 \sigma_a^2} \right) \, ds + 1 \]

Esta fórmula representa el valor esperado de \( U \) en el intervalo de tiempo desde \( T_0 \) hasta el infinito, donde \( U \) es el spread cointegrado, \( \phi \) es el coeficiente cointegrado, \( \sigma_a \) es la desviación estándar del proceso AR(1), \( E_{T_{0,\infty}}[U] \) es el valor esperado del spread \( U \) desde \( T_0 \) hasta el infinito, y \( E_{T_{0,b}}[s] \) es el valor esperado de \( s \) en el intervalo de tiempo desde \( T_0 \) hasta \( b \).

Claro, aquí tienes la adaptación:

\[ E_{T_{-\infty,U}}[0] = \lim_{{b\to-\infty}} \frac{1}{-b} \int_{-b}^{U} E_{T_{-b,U}}[s] \exp \left( -\frac{s^2}{2 \sigma_a^2} \right) \, ds + 1 \]

Esta fórmula representa el valor esperado de \( 0 \) en el intervalo de tiempo desde \( -\infty \) hasta \( U \), donde \( U \) es el límite superior del spread, \( \sigma_a \) es la desviación estándar del proceso AR(1), \( E_{T_{-\infty,U}}[0] \) es el valor esperado de \( 0 \) desde \( -\infty \) hasta \( U \), y \( E_{T_{-b,U}}[s] \) es el valor esperado de \( s \) en el intervalo de tiempo desde \( -b \) hasta \( U \).

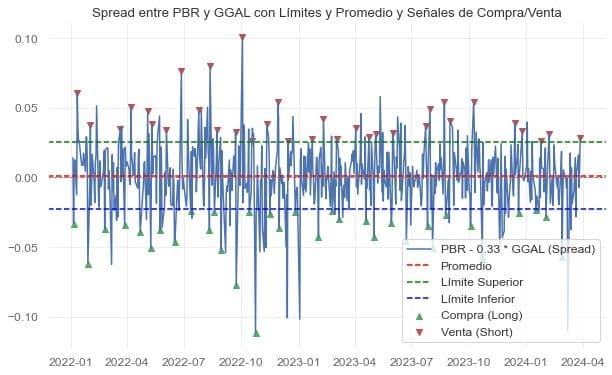
Entonces, concluyendo, podemos inferir que, a través del cálculo del spread de dos pares de activos cointegrados, al cual podemos establecerle límites superiores e inferiores y un promedio. Condicionando que, si el spread es mayor al límite superior se ejecuta una orden de venta o short para uno de los activos mientras que para el otro se ejecuta una orden de compra, y viceversa. Quedando concluida o cerrada tal orden cuando el spread es menor, en este caso al promedio histórico.

El uso de las LSTM en esta aplicación, se estructura de la base que, en lugar de trabajar con precios históricos para la ejecución de las operaciones, podemos utilizar las predicciones del modelo entrenado con redes neuronales, para anticiparnos y construir con un intervalo de confianza determinado un futuro probable antes de ejecutar nuestras órdenes, de esta forma podemos darle más tiempo y anticipación a nuestro modelo de ejecución que en lo posible, debería estar automatizado.

¿Qué quiere decir todo esto? Que si el modelo LSTM, arroja que la próxima predicción estará por encima o por debajo del umbral, definido este por la desviación estándar del spread, el algoritmo ejecute hoy la orden de mañana.

NOTA: La construcción del modelo LSTM debería ser testeado con minuciosidad y profundidad, ya que debería predecir y emular lo máximo posible el spread original de los dos pares de activos cointegrados.

Así mismo, la estrategia de trading dependerá de muchos factores no mencionados aquí como la optimización de la desviación estándar del spread, la administración de riesgo, la investigación profunda de si los activas están cointegrados o no, el tamaño de la posición, la volatilidad del mercado en el momento, etc.

Disclaimer: Este post es de apreciación personal, con fines educativos e informativos, no es para nada y bajo ningún concepto una estrategia de trading rentable o recomendación de compra o venta de activos financieros.