Optima Consulting & ManagementUso de KNN y LSTM para predecir volatilidad diaria
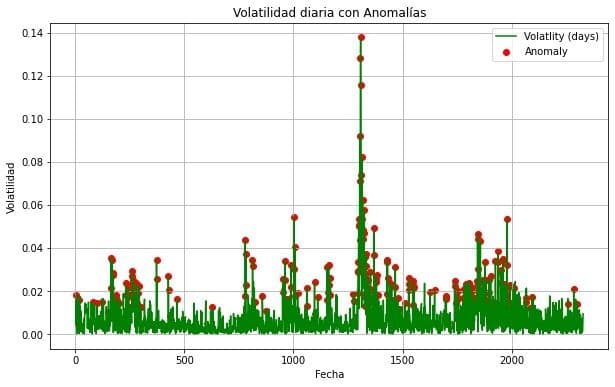
La volatilidad diaria de un activo financiero se puede calcular utilizando el precio de cierre del activo en diferentes días. Una medida comúnmente utilizada para la volatilidad es la desviación estándar de los retornos diarios. La ecuación para calcular la volatilidad diaria �diariaσdiaria de un activo se puede expresar de la siguiente manera:
σ diaria=raíz cuadrada(1/N∑i=1N(ri−rˉ)2)
Donde:
- N es el número total de días considerados.
- ri es el retorno diario del activo en el día �i.
- ˉrˉ es el retorno promedio diario del activo durante el período considerado.
El retorno diario ri se puede calcular como:
ri = Pi−1Pi− / Pi−1
Donde:
- Pi es el precio de cierre del activo en el día �i.
- Pi−1 es el precio de cierre del activo en el día anterior.
Una vez que se calculan los retornos diarios para cada día en el período considerado, se puede calcular la desviación estándar de estos retornos para obtener la volatilidad diaria del activo. La volatilidad diaria indica la magnitud de las fluctuaciones de precios del activo en un día determinado.
Una vez, hecho el cálculo de la volatilidad diaria, podemoos pasarle este cálculo a un modelo KNN, usando la librería Sklearn, from sklearn.neighbors import NearestNeighbors.
En el código se implementa un modelo de vecinos más cercanos (KNN) para detectar anomalías en un conjunto de datos. Aquí está la explicación paso a paso:
1. Entrenar el modelo KNN:
- Se define el número de vecinos más cercanos como `k = 5`.
- Se crea una instancia del modelo KNN utilizando la clase `NearestNeighbors` y se ajusta a los datos de entrada `X` utilizando el método `fit()`.
2. Calcular la distancia media de los k vecinos más cercanos para cada punto:
- Se utilizan los datos de entrenamiento `X` para calcular la distancia media de los `k` vecinos más cercanos para cada punto.
- Esto se logra llamando al método `kneighbors()` del modelo KNN, que devuelve las distancias y los índices de los k vecinos más cercanos.
- Luego, se calcula la distancia media para cada punto tomando el promedio de las distancias de los vecinos más cercanos a través de `np.mean()`.
3. Definir un umbral para detectar anomalías:
- Se define un umbral para detectar anomalías basado en un percentil de las distancias medias.
- En este caso, se utiliza el percentil 90 de las distancias medias como umbral.
- Esto se calcula utilizando `np.percentile()`.
4. Clasificar las volatilidades como normales o anormales:
- Se asigna una etiqueta de anomalía a cada punto en el conjunto de datos.
- Si la distancia media de los k vecinos más cercanos de un punto es mayor que el umbral definido, se etiqueta como una anomalía (1), de lo contrario se etiqueta como normal (0).
- Esto se logra utilizando `np.where()`.
Para resumir un poco, este código proporciona un enfoque simple pero efectivo para detectar anomalías en un conjunto de datos utilizando el algoritmo de vecinos más cercanos. Las anomalías se identifican mediante la comparación de la distancia media de los vecinos más cercanos con un umbral predefinido, que no es tan minucioso para poder,a modo de ejemplificación ver mejor las anomalías.
Luego, visualizamos los resultados del modelo con la librería matplotlib.pyplot.
Teniendo esto detallado y visualizando además, métricas del entrenamiento del modelo KNN, como el Accuracy, el F1 Score, etc. Le vamos a pasar la volatilidad calculada con los retornos diarios del activo a una Red Neuronal Recurrente (RNN).
Aquí, este resumen de la arquitectura de una red neuronal recurrente (RNN) con una capa LSTM (Long Short-Term Memory) seguida de capas densas (fully connected) en un modelo de aprendizaje profundo. Aquí los detalles a saber:
- Capa LSTM (lstm): Esta capa LSTM tiene una salida de forma (None, 300) y contiene 362,400 parámetros.
- Capa densa (dense): Después de la capa LSTM, hay una capa densa con una salida de forma (None, 300) y 90,300 parámetros.
- Capa de dropout (dropout): Esta capa de dropout tiene una salida de forma (None, 300) y no tiene parámetros entrenables.
- Capa densa (dense_1): Otra capa densa sigue a la capa de dropout con una salida de forma (None, 300) y 90,300 parámetros.
- Capa densa final (dense_2): La última capa densa tiene una salida de forma (None, 1) y 301 parámetros, que representa la salida final de la red.
En resumen, el modelo tiene un total de 1,629,905 parámetros, de los cuales 543,301 son entrenables. Los parámetros no entrenables corresponden a la configuración de la capa de dropout. Los parámetros del optimizador son adicionales y suman 1,086,604.
También podemos ver, la arquitectura de la red neuronal en términos matemáticos:
1. Capa LSTM (lstm):
- La salida de esta capa LSTM se calcula mediante la fórmula:
ht = LSTM(xt,ht−1)
-Donde xt es la entrada en el tiempo t, ℎht es la salida en el tiempo t, y ℎ−1ht−1 es el estado oculto anterior.
- La forma de la salida es (None, 300), lo que significa que para cada ejemplo en el lote (batch), hay 300 unidades en la salida.
2. Capa densa (dense):
- La salida de esta capa densa se calcula mediante la multiplicación de la entrada por una matriz de pesos y sumando un sesgo:
y=ReLU(Wx+b)
- Donde x es la entrada, W es la matriz de pesos, b es el sesgo e, y es la salida.La forma de la salida es (None, 300), similar a la entrada de la capa LSTM.
3. Capa de dropout (dropout):
- Esta capa aplica el dropout a la salida de la capa densa anterior para prevenir el sobreajuste.
- Matemáticamente, durante el entrenamiento, se anula aleatoriamente un porcentaje de las unidades de la salida, mientras que durante la inferencia, la salida se escala por el inverso del porcentaje de dropout aplicado durante el entrenamiento.
4.Capa densa (dense_1):
- Similar a la capa densa anterior, calcula la salida aplicando una función de activación ReLU a la entrada multiplicada por una matriz de pesos y sumando un sesgo.
5. Capa densa final (dense_2):
- Esta capa calcula la salida final de la red.
- Aplica una función de activación sigmoide para obtener una salida en el rango [0, 1], que se utiliza comúnmente para problemas de clasificación binaria.
Los parámetros totales, entrenables y no entrenables están relacionados con las matrices de pesos y sesgos de las capas densas, así como con los pesos específicos de la capa LSTM.
Una vez entrenado el modelo, lo utilizamos para poder asociar las predicciones a todo el conjunto de datos. Añadiendo las predicciones a un DataFrame donde podamos visualizar las predicciones del modelo LSTM, junto a los datos originales desescalados. Y de esta forma poder visualizar el conjunto de datos original, con la predicción del modelo.
La utilidad de esto, es, poder anticiparse mediante la predicción de la volatilidad diaria del ETF, SPY, a anomalías que puedan llegar a ser desconcertantes para el manejo de nuestro portfolio de inversión, o aumentar el riesgo al que estamos dispuestos a exponer nuestro manejo del dinero, afectando en consecuencia nuestra administración de riesgo.
Disclamer: Este post es de apreciación personal y a título informativo, no es bajo ningún concepto recomendación de compra o venta de activos financieros, mucho menos un sistema de trading, ya que esto implica administración de riesgo, diseño del sistema, arquitectura del backtest e implementación de las predicciones para operar.
Este post fue hecho por Gabriel Guardia, co fundador de Optima Consulting & Management LLC.
LinkedIn: www.linkedin.com/in/gabriel-gastón-guardia-a77a10183